Proudění plynů a par - termomechanika

TERMOMECHANIKA
Title

Proudění plynů a par
Řešené příklady
Příklad 9.5
Při zkujňování oceli foukáním kyslíku nad hladinu, je v zařízení umístěna dýza, kterou má protékat 1,1 kg.s-1
kyslíku. Stav kyslíku před dýzou je dán tlakem 0,9 MPa a teplotou 25 °C, tlak v peci je přibližně 0,1 MPa. Navrhněte dýzu tak, aby byla rychlost vytékajícího kyslíku maximální. Vrcholový úhel dýzy volte α = 10 °.
kyslíku. Stav kyslíku před dýzou je dán tlakem 0,9 MPa a teplotou 25 °C, tlak v peci je přibližně 0,1 MPa. Navrhněte dýzu tak, aby byla rychlost vytékajícího kyslíku maximální. Vrcholový úhel dýzy volte α = 10 °.
Předpoklad: Vstupní rychlost do dýzy je možno zanedbat, kyslík se chová jako ideální plyn (κ = 1,4; r = 260 J/(kg.K))
p1 = 0,9 MPa = 900 000 Pa
t1 = 25°C = 298,15 K
p2 = 0,1 MPa = 100 000 Pa
w1 = 0 m/s
Návrh dýzy:
S1,w1,v1,T1,
ρ1,p1
dk, wk, w2, d2, l = ??
Sk,wk,vk,Tk,
ρk,pk
S2,w2,v2,T2,
ρ2,p2
O2 – ideální plyn
α = 10°
κ = 1,4
r = 260 J/(kg.K)

Jedná se o průtok nadkritický nebo podkritický? – provedeme kontrolu tlakových poměrů
vzorce z úvodu kapitoly:
Provedeme kontrolu:
Přepočet na kritický průřez - v zadání máme, že kyslík se chová jako ideální plyn a jedná o isoentropickou stavovou změnu, a proto můžeme psát:
Výpočet kritické rychlosti provedeme pomocí vzorce z úvodu kapitoly, přičemž budeme reflektovat podmínku zanedbání vstupní rychlosti:
kde cp si vyjádříme pomocí Mayerova vztahu a vztahu pro Poissonovo číslo z úvodní kapitoly, jedná se o soustavu dvou rovnic, z níž vyjádříme tepelnou kapacitu jako:
Kritická rychlost potom je:
Měrný objem v kritickém místě je:
kde tlak jsme vypočítali z prvního vzorce.
Kritický průřez poté vypočteme jako:
Průměr dýzy dk je tedy:
Přepočet na výtokový průřez
Víme, že jde o IP a isoentropickou stavovou změnu, proto pro výpočet teploty použijeme klasický vzorec pro danou změnu:
Rychlost, objem, průřez a průměr vypočteme analogicky:
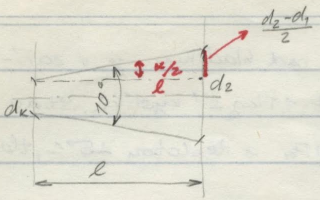
Délku rozšiřující se části dýzy vypočítáme dle znalosti goniometrie: